
XLI Olimpiada Matemática Española
OMG 2005
sábado 15 de xaneiro de 2005

 |
XLI Olimpiada Matemática EspañolaOMG 2005sábado 15 de xaneiro de 2005 |
 |
Problema 4 . Determinar todos os pares de números enteiros, x e y, (x < y) tales que a suma de todos os números enteiros comprendidos estrictamente entre ambos é igual a 2005.
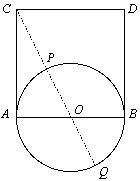
Problema 5 . Dada unha circunferencia de radio 1 e centro O, polo diámetro AB levántase un cadrado ABCD. Denotamos por P e Q as interseccións da recta que pasa por C e O con esta circunferencia . (ver figura) Probar que AQBP é un rectángulo áureo, é dicir,
|
 |
Problema 6 . Os números 1, 2, 3,..., 15 e 16 distribúense nas casiñas dun taboleiro de 16 filas por 16 columnas. Se cada un dos números se utiliza exactamente 16 veces, demostrar que sempre haberá unha fila ou unha columna na que aparezan polo menos catro números.